Последнее обновление: 8 Января 2022 г.

Как определить радиус горизонта?

Радиус горизонта – это, собственно, расстояние от человека. смотрящего в сторону горизонта, до границы горизонта. Т.е. это расстояние, в пределах которого человек способен разглядеть поверхность земли, в том числе, с использованием различных оптических приспособлений, например, бинокля или телескопа.

Формула для расчета радиуса горизонта

Предположим, что Земля имеет точную форму шара с радиусом, равным 6500 км.

Понятно, что в реальности это, зачастую, не так. В реальности форма земли не шарообразна, даже придумали специальный термин, при помощи которого обозначают форму Земли: геоид. Это. как бы сказать, шар, который слегка сплюснут у полюсов.

Кроме того, поверхность Земли редко является ровной. На ней нередко имеются то впадины, овраги, то возвышенности – холмы и горы. Строго говоря, более-менее шарообразной поверхность Земли является только в водных объектах - в морях или океанах. Если не считать наличия волн, конечно.

Но, для обобщенных расчетов, считая Землю строго шарообразной, получим формулу для расчета расстояния до горизонта. Приведем рисунок, чтобы было яснее.

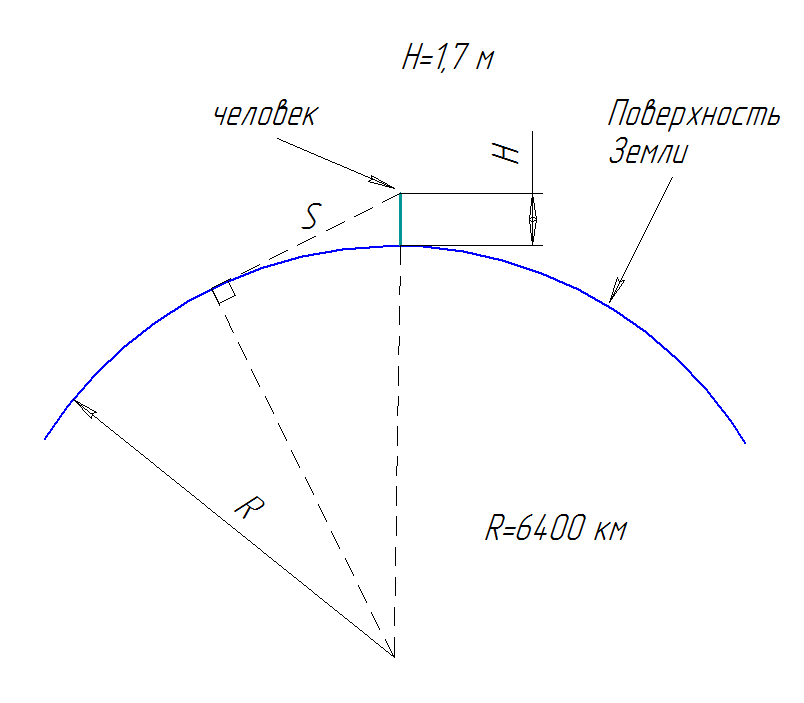
Допустим, рост человека составляет Н=170 см или 1,7 метра.

Тогда, очевидно пользуясь теоремой Пифагора, составляем соотношение:

R²+S² = (R+H)²

или

S² = 2RH+H²

Так как рост человека Н гораздо меньше, чем радиус земли R, то приближенно, но с хорошей степенью точности, можем записать:

S² = 2RH

Отсюда расстояние от глаз человека, вертикально стоящего на поверхности Земли, до линии горизонта, определится как

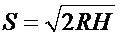
Это – формула для расчета радиуса горизонта на Земле, равно как и на любой другой планете, звезде, т.д. Подставив в нее рост человека и радиус земли, получим:

S_Земли  = (2*6400*10³*1,7)^1/2 = 4664 метра или 4,7 км.

Итак, на Земле, если ее поверхность не содержит гор, холмов, впадин, лесов и иных преград, а является идеально шарообразной, человек ростом 1,7 м сможет увидеть не дальше, чем на 4,7 км. Это и есть радиус горизонта на земле.

Для примера, рассчитаем радиус горизонта на Луне

Радиус Луны составляет 1700 км. Тогда радиус горизонта на Луне составит

S_Луны = (2*1700*10³*1,7)^1/2 = 2404 м или 2,4 км.

Что, в принципе, тоже на так уж мало. Хотя, наверное, космонавту, оказавшемуся на Луне, будет немного непривычно, особенно с первого раза. В самом деле – куда ни глянь, а НЕТ привычного охвата, масштаба расстояний. И взор будет обрываться всего лишь через 2,4 км… Это, наверное, как минимум, неуютно. Ощущение некоей ограниченности, что ли. Правда, опять же, наличие гор/впадин и иных неровностей рельефа может создавать впечатление земного рельефа и линия горизонта уже не будет играть существенной роли.

Впрочем, где-нибудь на астероиде, размером со средний российский город - и хуже того. Куда ни кинь взгляд - а места-то мало, вообще нет. Вокруг - лишь малый клочок суши. И - космос, космос, космос...